인장시험에서는 단순히 시편에 작용하는 인장응력이 재료의 일축항복응력 Y에 도달하면 재료가 소성변형을 시작하게 된다. 그러나 보다 복잡한 응력상태하에서는 재료의 항복 여부를 판단하기 위하여 재료에 작용하는 응력 성분들과 재료의 일축항복응력 사이의 관계를 명확히 할 필요가 있다. 이러한 관계를 항복조건(yield criterion)이라고 한다. 금속재료들의 경우 가장 보편적으로 사용되는 항복조건은 최대전단응력조건 (maximum-shearstress criterion)과 전단변형에너지조건(distorsion-energy criterion)이다.
여기에서는 재료가 연속이고, 균질이며, 등방성(isotropic)이라고 가정한다. 또한 인장응력은 양이고, 압축응력은 음이며, 재료의 인장항복응력과 압축항복응력의 크기는 같다고 가정하기로 한다.
[최대전단응력조건]
이 조건은 Tresca 항복조건이라고도 하며, 어떤 요소의 최대전단응력이 임계치에 도달할 때 항복이 시작된다는 가설에 근거하고 있다. 이때 전단응력의 임계치는 재료의 물성치로 재료의 전단항복응력(shear yield stress) 라고 한다. 즉, 항복시에는 재료 내의 응력상태가 다음 조건을 만족한다.
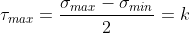
어떤 응력상태에서의 최대전단응력은 모어(Mohr) 응력원을 이용하거나 응력변환 공식을 이용하여 구할 수 있다. 최대전단응력이 k와 같으면, 이 응력상태를 갖는 소재는 항복된 상태에 있다고 본다. 식에서 최대수직응력과 최소수직응력의 차는 가장 큰 모어 응력원의 지름이 되며, 따라서 최대전단응력의 2배가 된다. 3개의 주력값들에서 중간값은 항복에 영향을 주지 않는다. 상기 공식의 왼쪽 항은 소재에 가해진 응력상태를 나타내고, 오른쪽 항은 소재의 물성치를 나타내고 있다.
전단항복강도와 일축항복강도 사이의 관계는 단순인장시험으로부터 다음과 같이 주어진다.

[전단변형에너지조건]
폰 미저즈(von Mises) 항복조건으로도 알려진 이 조건은 재료의 일축항복응력 Y와 소재에 가해진 응력성분들 사이에 다음과 같은 관계식이 만족되면 항복이 시작된다고 본다.
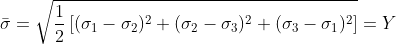
여기서 σ1, σ2, σ3는 각각 세 주응력을 나타낸다. 최대전단응력조건과는 달리, 이 조건식에는 주응력의 중간값도 포함되어 있다. 상기 공식에서 왼쪽 항은 소재에 가해진 응력상태를 나타내며 유효응력(effective stress)이라고 한다. 즉, 전단변형 에너지조건은 소재에 가해진 유효응력이 소재의 물성치인 일축항복응력과 같아질 때, 항복이 일어난다고 보는 것이다. 유효응력은 응력성분값들을 일축인장상태에 상당되는 응력값으로 나타내므로, 이를 상당응력 또는 대표응력이라고도 한다.
마찬가지로, 어떤 요소의 변형률 상태를 나타내기 위한 수단으로 다음과 같이 유효변형률(effective strain)을 정의한다.

일축인장상태에서는 유효변형률이 인장방향 변형률과 같게 된다. 따라서, 유효변형률을 상당변형률이라고도 한다. 전단변형 에너지조건을 따르는 재료의 전단항복응력과 일축함복응력 사이에는 다음과 같은 관계가 있다.
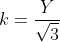
[항복조건의 검증]
각 항복조건들의 타당성을 입증하기 위한 각종 실험적 연구에서 보편적으로 사용되는방법은 얇은 원통형 시편에 내압이나 비틂하중을 가하거나, 두 가지 하중을 동시에 가하여 항복을 일으키는 하중의 크기를 구하는 것이다. 이로써, 하중의 형태에 따라 주응력간의 비율이 다른 평면응력상태를 얻을 수 있다.
소재가 평면응력상태에 있을 때(σ3=0), 앞에서 설명한 두 가지 항복조건들을 다음 그림에 곡선으로 표시하였다.
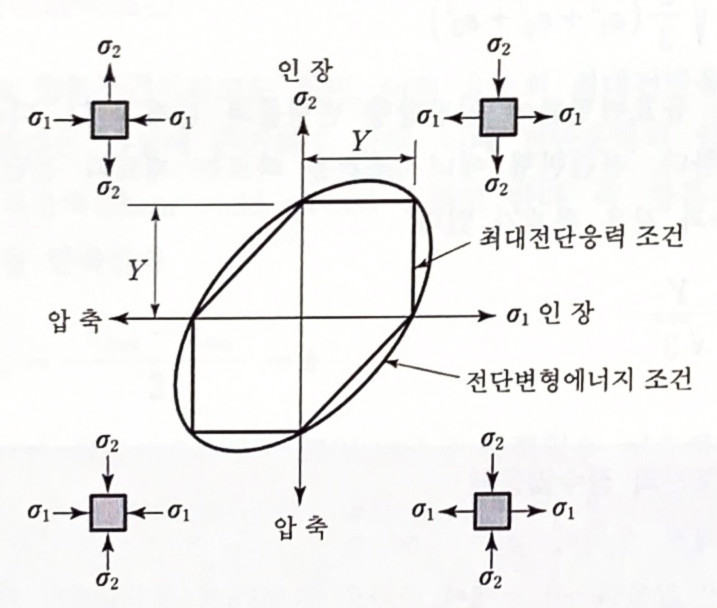
다양한 종류의 연성재료들의 항복거동에 대한 실험에 의하면,전단변형 에너지조건이 최대 전단 응력조건보다 실험결과에 더 잘 일치한다. 따라서, 연성재료를 취급하는 금속가공공정의 해석에는 전단변형 에너지조건의 사용이 바람직함을 알수 있다.
[유동법칙]
삼차원 탄성응력-변형률의 관계는 일반화된 후크의 법칙으로 나타낸 바 있다. 재료의항복 이후에 소성변형이 진행되는 동안의 응력-변형률관계는 유동법칙(flow rule)으로 나타낼 수 있다. 유동법칙은 다음과 같이 변형률증분의 형태로 나타낸다.

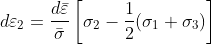
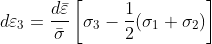
평면변형률상태가 유지되는 경우에는 ε2 = 0이 되므로, 중간응력인 σ2는 다음과 같이최대주응력과 최소주력의 산술평균이 된다.
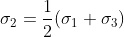
[체적변형률]
일반화된 후크의 법칙을 나타내는 다음 식들을 합하면,
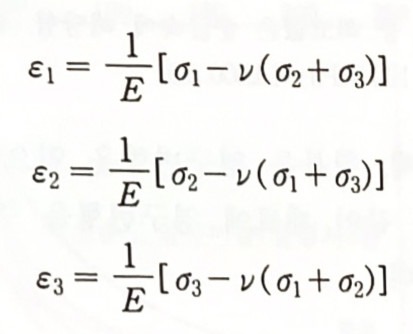
다음과 같이 탄성변형시의 체적변형률(volume strain) 또는 팽창률(dilatation) ευ에 관한 식을 얻는다.

상기 공식으로부터 알 수 있듯이, 탄성영역에서는(0 < ν < 0.5) 인장시편의 체적은 증가되고 압축시편의 체적은 감소된다. 재료의 체적탄성계수(bulk modulus) K는 다음과 같이 정의된다.

여기서 σm는 평균응력(mean stress) 또는 정수압응력(hydrostatic stress)이라 하며 다음과 같이 정의된다.
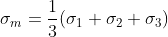
금속재료의 소성변형영역에서는 체적변화가 없음이 실험적으로 확인되어 있다. 따라서 소성가공시에는 ν = 0.5라고 볼 수 있고, 다음 식이 성립된다.
εν = ε1 + ε2 + ε3 = 0
이 조건은 소성변형시에 두 변형률들을 알고 나머지 한 변형률을 구할 때 편리하게 사용된다.
'전공 기본 > 기계재료' 카테고리의 다른 글
| 재료의 가공특성 (5) - 변형에 따른 불안정성 (0) | 2022.09.12 |
|---|---|
| 재료의 가공특성 (4) - 응력-변형률곡선 (0) | 2022.09.10 |
| 재료의 가공특성 (2) - 인장시험과 소재의 변형거동 (0) | 2022.09.07 |
| 재료의 가공특성 (1) (0) | 2022.09.04 |
| 기계재료 (6) - 세라믹재료 (0) | 2022.09.03 |




댓글