접촉경계면에서의 마찰이 없고 재료가 항복응력 Y를 갖는 완전소성체이면 원주시편에 작용하는 수직압축응력은 Y로일정하다. 이 경우에는 이상변형(ideal deformation)만 일어나게 된다. 임의의 높이 h1에서의 가공력은
F = YA1
이며, 이는 이상변형만을 가정하였으므로, 소재를 압축하기 위한 최소하중을 나타낸다고 할 수 있다.재료가 변형경화성이면,항복응력 대신에 유동응력 Yf를 사용하면 된다. 실제의 단조하중은 마찰일과 과잉일이 포함되므로 상기 식으로 계산되는 값의 수 배에 달한다.
A1은 소재의 단면적으로, 체적이 일정하다는 조건으로부터 다음과 같이 계산할 수 있다.

변형일은 다음과 같이 시편의 체적과 비에너지 u의 곱으로 나타낼 수 있으며,

여기서 e1은, 다음 식으로 구한다.

따라서, 다음 식으로 표현되는 변형경화성 재료의 경우,

가공일은 다음과 같이 계산된다.

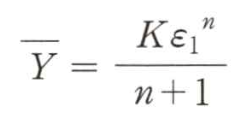
이상변형일에 마찰일을 추가로 고려하여 단조하중을 계산하려면 슬래브해석 결과를 이용할 수 있다. 원주압축의 경우, 압력분포, 평균압력, 압축하중은 각각 다음과 같이 요약된다. 단, 이들 식에서 a는 소재의 반지름, h는 높이를 나타낸다.



압력분포는 소재와 금형간의 상대속도가 바뀌는 지점(r = 0)에서 압력이 최대인 양상을 보여주며, 이를 마찰언덕이라고 하였다. 소재의 부피는 일정하므로, 단조가 진행됨에 따라 a/h비는 급격히 증가하게 된다. 해석결과로부터, a/h비와 마찰력이 접촉압력과 단조하중에 미치는 영향이 중요함을 알 수 있다.
평면변형률 압축의 경우에도 평면변형률조건 항복응력 Y'를 사용하여, 위와 비슷한 식이 얻어진다. 즉, 소재의 금형접촉길이의 절반을 a, 높이를 h라 하면,

직육면쳬인 소재를 압축하는 경우에 나타나는 마찰언덕은 다음 그림 (a)와 같으며, 소재와 금형간의 마찰로 인해 접촉면의 변형양상은 다음 그림 (b)와 같다.

상기 식에서 변형경화성 재료에 대해서는 Y대신 유동응력 Yf를 사용하면 된다.압력분포식에서 마찰계수 μ는 냉간단조의 경우 0.05-0.1, 열간단조에서는 0.1-0.2 정도이다. 보다 정확한 값은 윤활제의 효율에 따르며, 특히 소재면에서 윤활막이 끊긴 경우에는 이보다 높을 수 있다. 업세팅에서 마찰과 시편의 형상비(a/h)가 평균압력 Pavg에 미치는 영향을 상기 그래프 그림에 나타내었다. 압력은 무차원 형태로 항복응력의 배수로 나타내었으며, 평면변형률 압축의 경우에는 Y 대신 Y' 이 사용되었음에 유의하자.
※ 고착조건에서의 단조
원주압축이나 평면변형률압축에서 μ와 p의 곱은 모두 마찰응력(표면전단응릭)으로, 중심부로 갈수록 압력 p가 증가하므로 μp도 증가한다. 그러나 μp의 값은 재료의 전단항복응력 k를 초과할 수 없다. μp = k가 되면, 고착(sticking)이 일어난다. 고착의 경우라 하더라도 경계면에서의 접착을 뜻하는 것이 아니고, 단지 재료가 압축판에 대하여 상대적으로 움직이지 않을 뿐이다.
축대칭조건과 평면변형률조건의 경우, 고착조건에서의 압력분포는 각각 다음과 같이 중심에서 떨어진 거리에 선형적으로 변한다.

'전공 기본 > 기계공작법' 카테고리의 다른 글
| 금속성형공정 - 단조 - 4. 기타 단조작업 (0) | 2023.09.12 |
|---|---|
| 금속성형공정 - 단조 - 3. 형단조 (0) | 2023.09.12 |
| 금속성형공정 - 단조 - 1. 자유단조 (0) | 2023.06.04 |
| 주조공정 - 주물의 설계 (0) | 2022.12.24 |
| 주조공정 - 주물 내 결함 (0) | 2022.12.24 |



댓글